2021. 7. 28. 21:43ㆍIT Study/Ai
이번에는 저번에 했던 RNN과 TimeRNN에 이어 TimeEmbedding,TimeAffine,TimeSoftmaxWithLoss를 만들고 이 모든걸 합쳐 RNNLM을 공부했다.
기본적으로 Time이붙으면 시계열 데이터를 처리하는 계층이라고 보면되는데 TimeRNN의 순차적인 forward로직의 포인트만 알고있으면 나머지 TimeEmbedding,TimeAffine,TimeSoftmaxWithLoss은 이미 저번에 배웠던 것에서 크게 변하는 것없이 구현가능하다.
TimeEmbedding
Embedding은 저번포스팅에 word2vec로직에서 나왔던 계층이다. 그 때는 단어의 분산표현을 저장할 가중치 행렬에서 단어의 인덱스를 받아 원하는 행을 뽑아오는 로직이였다.
이 TimeEmbedding또한 그 역할이 크게다르지않다. 역시 처음 인풋값으로 단어의 인덱스를 받아오고 Embedding이 가지고 있는 가중치 행렬에서 맞는 인덱스의 행을 빼서 RNN계층으로 넘겨주는 것 까지가 그 기능인데 여기서 인풋값이 시계열 데이터고 그로인해 출력값도 시계열 데이터로 넘겨주는 것이 포인트이다.
저번 word2vec하고의 차이점은 그럼 두가지인데 일단 학습의 목적이 다르다. wor2vec은 오로지 단어의 분산표현만을 목적으로 학습을 진행하지만 RNNLM에서는 단어의분산표현이 아닌 각각의 시계열데이터 바로 다음 시각의 단어의 확률을 얻는 것이 목적이다.
두번째는 당연하게도 형식의 차이이다. wor2vec의 Embedding계층은 한개씩 처리를 하지만 RNNLM에서의 Embedding은 시계열데이터라는 데이터 뭉치를 처리하게 된다.
이 TimeEmbedding계층이외의 다른계층은 별다른게 없어서 설명은 생략하겠다.
RNNLM
먼저 RNNLM의 전체적인 모습을 보자
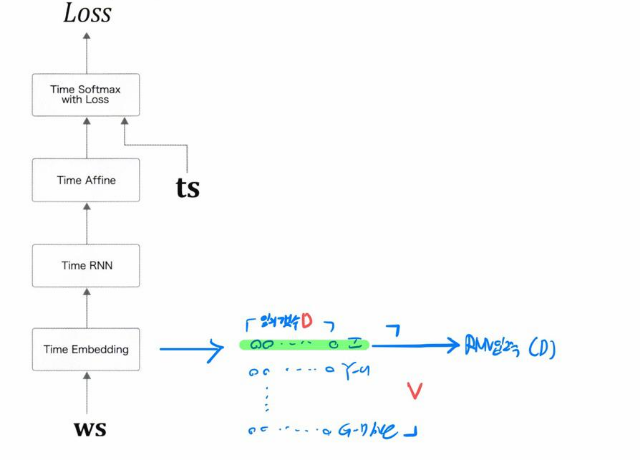
위에서 설명한대로 모델이 구성되어 있는 것을 볼수있다.
여기서 한가지 주의해야 할점은 TimeAffine이나 TimeEmbedding계층은 각자의 가중치를 가지고있는 계층이다.
그렇다면 RNNLM에서 모델이 학습될 때 이 계층들의 가중치는 어떻해 이루어 질까?
당연히 RNNLM에 포함되어있는 계층답게 아무리 시계열 데이터수가 많아도 모두 순환되며 같은 각각의 계층끼리 가중치가 모두 공유된다. 즉 RNNLM하나당 Embedding가중치 1개 TimeRNN 가중치2개 바이어스1개 TimeAffine 가중치1개 바이어스 1개로 이루어진 것이다.
RNNLM가중치 형상
항상 어떠한 모델을 만들 때는 가중치를 초기화해주는 생성자 함수로 시작을 한다. 그만큼 가중치의 형상은 중요하다 생각하고 이 가중치의 형상은 행렬의 형상공식을 바탕으로 손쉽게 구할 수 있다.
일단 이 RNNLM에서 필요한 인자들은
1. vocap_size // 단어의 index갯수 즉, 단어의 종류 수
2. wordvec_size // Embedding계층에서 사용될 차원의 수
3. hidden_size // 은닉계층의 차원의 수
이 세가지이다. 여기서는 편의를 위해
vocap_size = V
wordvec_size = D
hidden_size = H
라고 명해주겠다.
먼저 Embedding계층의 가중치 행렬부터 확인해보자.

위의 그림을 보면 바로 이해가 될 것이다. Embedding계층의 가중치 행렬의 형상은 V*D이다.
V는 너무나 확실하고 D는 조금 헷갈릴 수 있는데 이 D는 사용자가 직접 정의해주는 차원의 수이다. 여기서 D를 3으로하던 10으로하던 사용자의 자유인 것이다.
하지만 너무 차원을 작게하면 학습이 제대로 이뤄지지 않을 위험이 존재하고 너무 크게하면 최적화의 면에서 마이너스 적인 요소가 있다. 이런 하이퍼 파라미터는 여러번 시행착오를 통해 최적화된 수치를 찾아내는 것이 중요하다 할 수 있겠다.
Embedding계층에서 결론적으로 전달해주는 출력값은 입력된 인덱스에 맞는 한 행인 1*D의 행렬인 값이다.
두번 째로 RNN의 가중치 행렬을 확인해보자

Wx의 가중치의 형상은 임베딩에서 넘어오는 출력값의 형상과 우리가 설정한 하이퍼 파라미터인 은닉층의 형상으로 정해진다.
임베딩에서 넘어오는 행렬의 형상은 1*D 우리가 직접 설정해준 H를 통해 은닉층의 형상은 D*H가 될 것이다. 여기서 은닉층의 형상에서 D가 나온이유는 두 행렬을 합성곱 할때 1*D * D*H 와 같이 1식의 열과 2식의 행은 같은 모습이어야 하기 때문이다.
이렇게 되면 나머지는 간단하다 1*D * D*H = 1*H 라는 식이 도출 될 것이다. 식의 결과값은 1식의 행 2식의 열값이기 때문이다.
여기서 부터 쭉쭉 계산을 해나가면 합성곱이나 특수한 행렬의 모습을 변환시키는 식이 없으니 b역시 1*H 가 될 것이고
h(next),h(prev)역시 1*H 의 형상을 띄게 될 것이다.
그러면 마지막으로 Wh의 형상은 지금까지의 식으로 보아 h(prev)의 형상 1*H 결과값 1*H 를 통해 구할 수 있게된다.
식을 쓰게 되면 1*H * ㅁ*ㅁ = 1*H 인데 위에 설명한 행렬의 성질에 의하여 1*H * H*H = 1*H 라는 식이 도출된다.
결국 Wh의 형상은 H*H 라는 것이 나오게 되는 것이다.
마지막으로 Affine계층의 가중치를 계산해보자.
일단 입력값으로 1*H가 입력이 될 것이다. 그러면 Affine의 가중치 W의 행은 H가 확정이 되는 것 까지는 확실하다.
여기서 부터 조금 복잡해진다. 이 Affine계층의 출력값의 형상이 곧 W의 열 형태로 연결되는 것은 지금까지 잘 이해 했다면 충분히 인지가능할 것이다. 그렇다면 출력값의 형상은 정해져 있는 값인가? 정해져 있다면 우리는 W의 모습까지 완벽하게 파악할 수 있을 것이다. 미리말하자면 출력값의 형상은 정해져있다. 그 이유는 softmax의 특징에서 나타난다.
softmax의 출력값은 어떤 형태인가?
softmax는 다중분류를 할 때 사용되는 오차함수라고 익히 알려져있다. 그렇다면 softmax의 형태는 다중분류를 확률로 표현한 것이니까 우리 RNNLM의 입장에서는 모든 단어 종류를 확률로 출력을 할 것이다. 모든 단어의 종류 맞다. 즉 vocap_size, V 인 것이다. 그렇다면 softmax의 입력값또한 1*V 일 것이다. 그렇다면 Affine의 출력값도 1*V 이고
처음으로 돌아와서 1*H * ㅁ*ㅁ = 1*V 가 되는 것이다 그렇다면 행렬의 성질에 의해 Affine계층의 가중치는 H*V가 되는 것이다. 자연스럽게 b도 1*V가 되면 모든 가중치와 바이어스 형상을 나타낼 수 있다.
퍼플렉서티(perplexity)
퍼플렉서티는 언어모델의 성능을 평가하는 척도이다. 간단히 말해 확률의 역수라고 말할 수 있겠다.
예시를 하나 들어보자 RNN의 학습을 완료한 후 평가 단계에서 you를 입력을 했다고 가정을 하자.
you에 맞는 정답단어는 say이고 모델1에서는 softmax를 통해 say의 확률이 0.8이라고 산출이 되었다. 그렇다면 퍼플렉서티는 이 확률의 역수인 1.25가 되는 것이다.
그러면 만약 say의 확률이 0.2라고 산출한 경우는 어떨까? 그러면 퍼플렉서티의 값은 0.2의 역수인 5가 될 것이다.
이렇게 수를 산출하는 것은 간단하다. 그렇다면 이 수가 시사하는 것은 대체 무엇일까?
두번째 경우가 되게 직관적인 수치이다. 만약 say가 나올확률이 0.2라고 하면 나머지 0.8에대해서 생각을 해보는 것이다. 0.8은 0.2가 4개가 존재한다. 이를 해석하면 이 모델은 you뒤에 나올 정답단어의 경우의수가 5가지라고 말할 수 있는 것이라고 말할 수 있겠다. 이 5가지는 퍼플렉서티값인 0.2의 역수인 것이다.
우리는 그러면 이 퍼플렉서티 값을 모든 데이터에 적용을 해 평가로직에 적용할 수 있는 방법을 고안해야 한다.
여기에서는 공식을 쓰면 빠른데 모델의 평가를 할 때 나오는 오차를 활용하면 금방 구할 수 있게된다. 식의 내용은
perplexity = e**L 이라고 표현가능하다. 한번 공식을 도출해 보는 것도 좋은 경험일 것이다.
RNNLM의 배치처리와 Truncated BPTT의 관계
제목을 보고 이 두개의 연관성이 바로 떠오르게 되면 정말 칭찬을 아낄 수 없겠다. 이 두 기술을 말해보자면 배치처리는 300개의 데이터가 있을 때 컴퓨터의 빠른 연산을 위해 몇개단위씩 끊어 뭉치단위로 학습을 시키는 기술이다. Truncated BPTT는 전 포스팅에서 말했듯이 엄청나게 긴 시계열 데이터를 학습시킬 때 여러 문제(최적화,기울기소실)을 피하기 위해 몇몇 단위씩 끊어 뭉치단위로 만든뒤 학습과 역전파를 한다고 설명했다.
이 두 기술의 공통점과 가장 중요한 점은 뭉치단위로 학습을 시킨다는 것이다. 그렇다면 배치처리를 Truncated BPTT와 합칠 수 없을까가 논점인 것이다. 실제로 "밑바닥부터 시작하는 딥러닝2" RNNLM Trainer class은 get_batch함수와 fit함수를 통해 Truncated BPTT의 핵심인 끊어진 입력값을 만든다. 이 입력값은 학습이 진행되자마자 오차의 역전파가 진행이 된다. 배치하나가 끝나면 바로 다음 입력값으로 채워져 다음 학습을 진행한다 그리고 다음으로 이동하기전 역시 오차의 역전파가 진행이 된다.
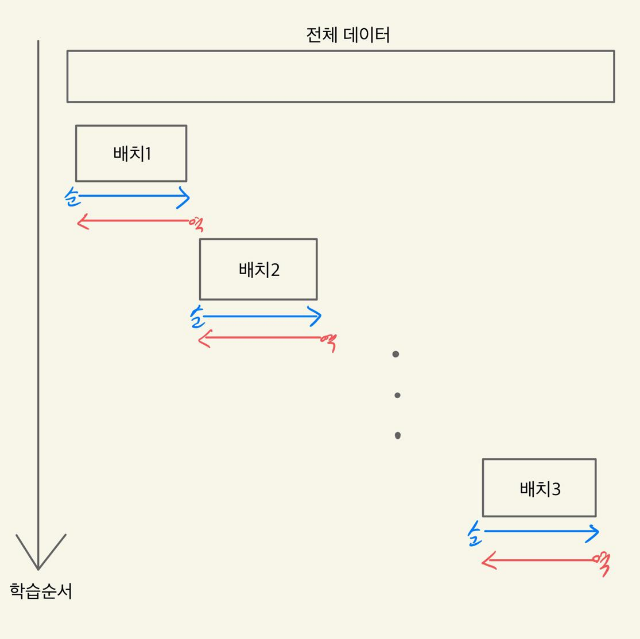
이런 모습으로 배치와 Truncated BPTT의 조합으로 우리가 원하는 목표를 쉽게 달성할 수 있게 된다.
출처 : 밑바닥부터 시작하는 딥러닝2
'IT Study > Ai' 카테고리의 다른 글
| Seq2Seq 개선 (Reverse, Peeky, Attention-어텐션) (0) | 2021.08.14 |
|---|---|
| seq2seq(Sequence to Sequence) (0) | 2021.08.04 |
| LSTM(Long Short-Term Memory) (0) | 2021.07.30 |
| RNN, Truncated BPTT, Time RNN (0) | 2021.07.27 |
| 자연어처리 Word2Vec 개념 (0) | 2021.07.18 |